Component in ZK-SNARK

Here are the main components of a ZK-SNARK.

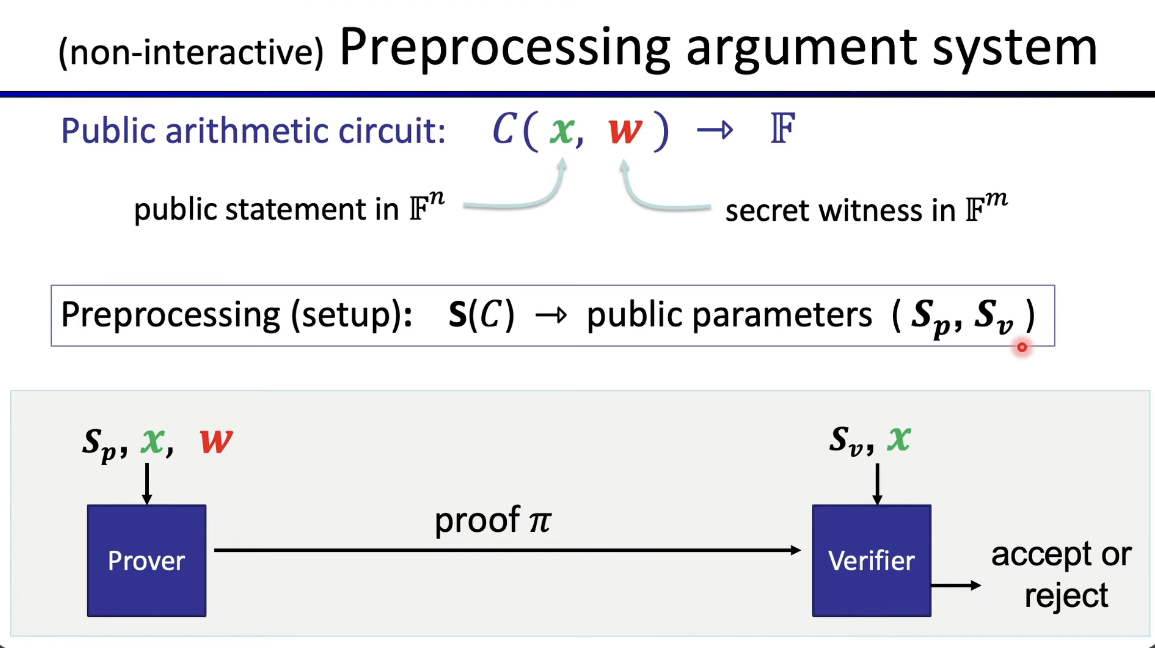
Component

Let's explain each component one by one.

  1. Circuit(C) = Arithmetic circuit
    • DAG (directed acyclic grahp)
    • An arithmetic circuit can be represented as an n-variate polynomial with an associated evaluation recipe.
    • |c| = gate of the circuit.
    • Writing in DHL language 👉 Circom
    • Number in Arithmetic circuit will be mod with finite field đ”Ŋ 👉 ECDH

Here is an example of a DAG (Directed Acyclic Graph) that illustrates this arithmetic circuit x1 * (x1 + x2 + 1) * ( x2 + 1)

    graph LR
    A[x1] --> Plus(+)
    B[x2] --> Plus(+)
    Constant[1] --> Plus(+)
    Constant[1] --> minus(−)
    B[x2] --> minus
    Plus(+) --> Product(*)
    A[x1] --> Product(*)
    minus(−) --> Product(*)
    Product(*) --> Result(x1 *īš™x1 + x2 + 1īšš * īš™x2 − 1īšš)

This circuit has three gates, and it will take inputs (x, w) to produce a proof

  1. X = Public statement

    • For example, I need to prove what 'a' is in this circuit (arithmetic circuit) a**3 + a + 5 == 35 This equation represents the statement.

  2. W = Secret withness

    • The thing you use to prove the statement is called the witness. For example, if you need to find the value of 'a' in the equation a**3 + a + 5 == 35 and the value of 'a' is 3, then '3' is your secret witness.

Relation of (X, W) for more example 👉 "W is the credential for account X", "W is secret key for public key X" etc.

  1. S(Setup algorithm) = Preprocessing

    • Why is setup needed? You can find a detailed explanation of the setup process here 👉 Setup explain ?
      • In essence, the setup acts as a pre-processing step that generates common parameters (summarize) for both the prover and verifier.
      • The setup process outputs two sets of parameters: (Sp) for the prover and (Sv) for the verifier.

  2. Prover

    • The prover's job is to convince the verifier that a specific value of W is valid.
    • The prover takes (Sp, X, W) as input.

  3. Verifier

    • The verifier receives a proof from the prover and determines whether to accept or reject it by returning a value of 0 (reject) or 1 (accept).