Hello Zero Knowledge

NinNin

NinNin is a Book Lab for ZK.

Written by supamongkon.r@gmail.com This book aims to introduce everyone interested in ZK technology and in need of an easy-to-follow guide to mastering it, beginning with the fundamentals.

Why do we need to learn this?

  • If you are interested in blockchain or are a developer, zero-knowledge (ZK) technology will become an increasingly important field since the day this book was published.

Book Structure

Begining πŸ₯š
Knowing 🐣
Doing πŸ₯
Experizing 🦦

Security Risk

  • While any system working with credentials or privacy involves some risk of unauthorized access, this book focuses on teaching you how to understand and write circuits, a fundamental skill for working with zero-knowledge proofs (ZKPs). ZKPs offer a way to prove information is true without revealing the information itself, which can be crucial for building secure and private systems. To learn more about the specific implementation details of circuits, I recommend referring to the official Circom documentation: RTFM

Furthermore, this book does not provide development advice.

Okay, let's learn!

What is ZK

At first you will understand that ZK technology is not blockchain, and you may wonder how blockchain use this technology

ZK

  • Cryptographic technique for proving knowledge (Privacy) aim for Privacy-preserving verification

Blockchain

  • Distributed ledger for transactions (Transparent) aim for Cryptocurrencies, Supply chain

This two thing is seerately difference approch, but ZK can use for bring privacy approch to public blockchain network like we saw in ternado cash. πŸ’ΈπŸŒͺ️

How it differ between ZK in public blockchain and Private Blockchain it's use same technology or not ?

Answer : No it not the same one

pls go to this Repository that I've to create 2 years ago to see how to make private blockchain using hyperledger besu and tessera.

and if you want some, or need to run private blockchain in you local pls visit this Repository

this is how besu and tessera work to send private transaction.

Image description

you will see in private network we need to setup another node call tessera to manage about privacy and also working along with libraly call Web3js-quorum

OK I'll don't go too much with private blockchain but the this is why in context of Privacy between Privacy with ZK and Privacy with private blockchain is difference.

ZK-SNARK

ZK technology is used for proving things without revealing any information. In other words, the system learns nothing about the information.

But in this book what we gonna learn is callZK-SNARK

Let's split the word SNARK
S = Succint
N = Non-interactive
ARK = Argement of Knowleage

it's quit seem confustion? but don't worry I'll explain step by step

Β  S (Succint) πŸ‘‰ Proofs must be short and fast to verify.

N (Non-interactive) πŸ‘‰ The prover sends a proof to the verifier in a one-way communication; therefore, the verifier does not respond to the prover, but only Accepts or Rejects it.

AR (Argement of Knowleage) πŸ‘‰ The prover tries to convince the verifier to process the proof without revealing anything about the secret witness.

Everything I have explained thus far pertains to this diagram, which we will use throughout this book to explain how ZK works.

Here is a simple flowchart to illustrate the process.

graph LR
A[Prover] --> B{Commits secret & statement}
B --> C{Generates challenge}
C --> A
A[Responds with proof] --> D{Verifies proof using commitment}
D -->|Proof valid?| E(Yes)
D -->|Proof invalid?| F(No)
E --> G{Grants access/verification}
F --> H{Rejects access}

Now you will see a brief overview of the actors or components in zk-SNARK. Next, we will delve into each actor in detail. Let's begin!

Component in ZK-SNARK

Here are the main components of a ZK-SNARK.

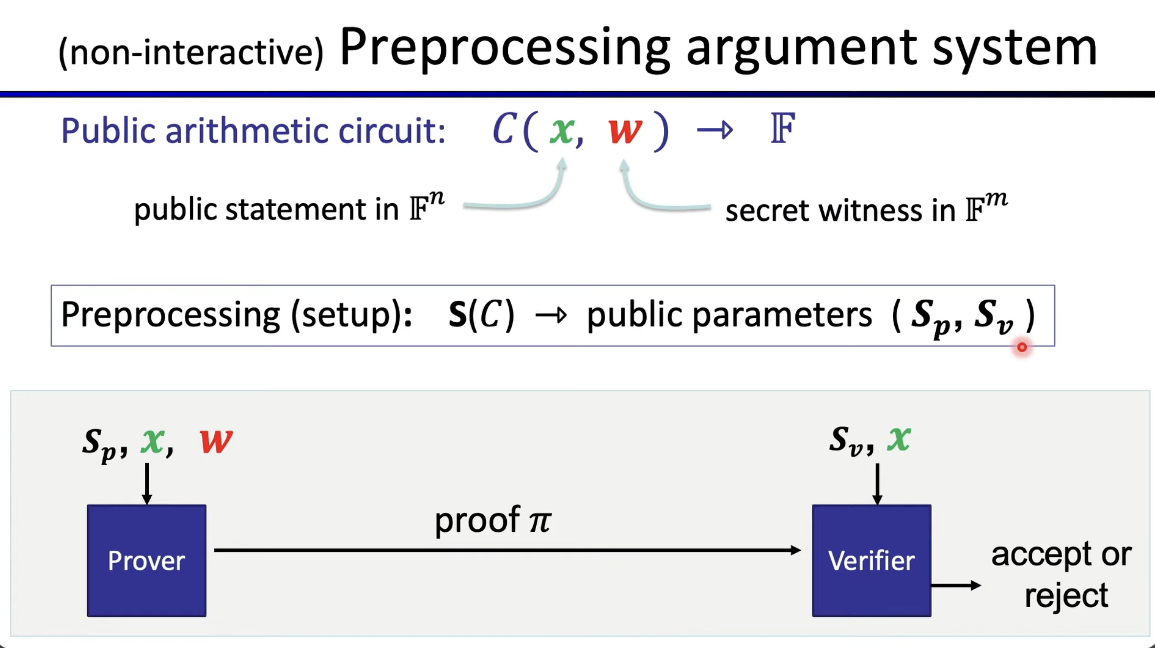
Component

Let's explain each component one by one.

  1. Circuit(C) = Arithmetic circuit
    • DAG (directed acyclic grahp)
    • An arithmetic circuit can be represented as an n-variate polynomial with an associated evaluation recipe.
    • |c| = gate of the circuit.
    • Writing in DHL language πŸ‘‰ Circom
    • Number in Arithmetic circuit will be mod with finite field 𝔽 πŸ‘‰ ECDH

Here is an example of a DAG (Directed Acyclic Graph) that illustrates this arithmetic circuit x1 * (x1 + x2 + 1) * ( x2 + 1)

    graph LR
    A[x1] --> Plus(+)
    B[x2] --> Plus(+)
    Constant[1] --> Plus(+)
    Constant[1] --> minus(βˆ’)
    B[x2] --> minus
    Plus(+) --> Product(*)
    A[x1] --> Product(*)
    minus(βˆ’) --> Product(*)
    Product(*) --> Result(x1 *οΉ™x1 + x2 + 1﹚ * οΉ™x2 βˆ’ 1﹚)

This circuit has three gates, and it will take inputs (x, w) to produce a proof

  1. X = Public statement

    • For example, I need to prove what 'a' is in this circuit (arithmetic circuit) a**3 + a + 5 == 35 This equation represents the statement.

  2. W = Secret withness

    • The thing you use to prove the statement is called the witness. For example, if you need to find the value of 'a' in the equation a**3 + a + 5 == 35 and the value of 'a' is 3, then '3' is your secret witness.

Relation of (X, W) for more example πŸ‘‰ "W is the credential for account X", "W is secret key for public key X" etc.

  1. S(Setup algorithm) = Preprocessing

    • Why is setup needed? You can find a detailed explanation of the setup process here πŸ‘‰ Setup explain ?
      • In essence, the setup acts as a pre-processing step that generates common parameters (summarize) for both the prover and verifier.
      • The setup process outputs two sets of parameters: (Sp) for the prover and (Sv) for the verifier.

  2. Prover

    • The prover's job is to convince the verifier that a specific value of W is valid.
    • The prover takes (Sp, X, W) as input.

  3. Verifier

    • The verifier receives a proof from the prover and determines whether to accept or reject it by returning a value of 0 (reject) or 1 (accept).

Basic Math for Zero-Knowledge

There is a lot of mathematics used in zero-knowledge technology, similar to cryptography.

However, in this section, we will focus on learning the mathematics necessary to understand how to write circuits and how these circuits function mathematically.

There are two sections of mathematics that you should be familiar with before diving into the code section.

Non-linear Equation

  • Why do we need to know this?
    • When we write circuits in Circom, they must be expressed in terms of quadratic equations. These constraints are essential for the efficient generation of zero-knowledge proofs.
  • Why must circuits in Circom be expressed in terms of quadratic equations?
    • Imagine if the minimum complexity of each computation were x ** 4. Computation time would skyrocket, leading to increased complexity and significantly longer processing times. This is why Circom restricts computations to a maximum of x ** 2 – it prioritizes efficient proof generation.

Linear vs Non-linear

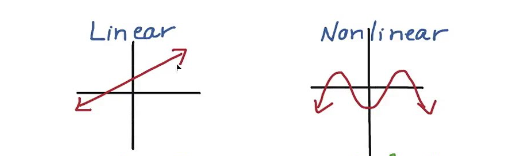
Graph

Matrix

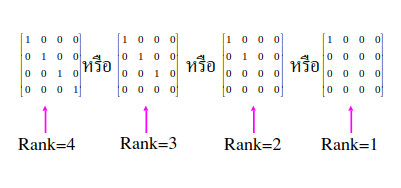
Rank of matrix

  • Why do we need to know this?
    • After wiring an arithmetic circuit, it will be compressed and computations will be expressed in terms of R1CS (Rank-1 Constraint System), which heavily involves matrix operations. 1

Why is it called "Rank-1"? - The rank of a matrix is used to evaluate how many independent equations can be derived from it. - Therefore, Rank-1 constraints are designed to efficiently compute and process only one independent equation per matrix. Imagine having 10 ranks in a matrix; the computational complexity would significantly increase.

Rank

solving equation problem with matrix

A common technique to determine the rank of a matrix and subsequently solve systems of equations is to use Gaussian elimination.

Negligible function

Known as a cryptographic method to improve the security of our proofs.

Definition (Please visit this video first) πŸ‘‰ https://www.youtube.com/watch?v=l5A3oEG-XKk&list=PLAj2bGZ0eFtICkway8SJBrJBQ76VinWzB&index=2

Imagine an attacker attempting to perform a brute-force attack with unbounded computational resources to find our proof in the field 𝔽.

So, what happened?

Brute force will not work effectively because finding the correct 'N' would take an extremely long time. This means that the attacker is effectively limited to polynomial time, whereas the proof verification can be accomplished in logarithmic time.

Then, the attacker would resort to a guessing method, often referred to as a poly-bounded adversary, to attempt to select the correct value.

This is where negligible functions come into play.

A polynomial-time algorithm has 'n' as a secret parameter. This means that if an attacker needs to find the correct value, they would be limited to polynomial time complexity. However, they might employ a method to randomly select potential values for 'n', which could potentially increase the time required for a successful attack.

what negligible function do ?

  • significantly reduce the probability of finding the correct value within polynomial time.

  • Negligible functions define an upper bound on the probability of an event occurring within a reasonable timeframe, especially in the context of cryptography. For example, in the scenario where an attacker attempts to guess a secret parameter within polynomial time, a negligible function would define an upper bound on the probability of the attacker successfully finding the correct value. cuz it think about 1 / p(Ξ»)

This is why the proof size depends on Ξ» (the secret lambda parameter).

Proof size

Rank 1 Constrain Systems

Now, after compiling your circuit, you obtain a file.r1cs file. This indicates that the part where matrix operations come into play has begun.

This is the definition of R1CS. Az * Bz - Cz = 0 or Az * Bz = Cz

where A, B, and C are matrices representing the circuit.

and w is how to compute witness in term of

  • (1 || x || w)

and then perform an element-wise product (multiplying 'w' with A, B, and C index by index)

Matrix definitiion

Here are some code examples of how to convert arithmetic circuits to R1CS.

out = x * y + 2

Optimize to prevent the R1CS file from becoming larger than necessary.

out - 2 = x * y

import numpy as np
import random

# Define the matrices
A = np.array([[0,0,1,0]])
B = np.array([[0,0,0,1]])
C = np.array([[-2,1,0,0]])

# pick random values to test the equation
x = random.randint(1,1000)
y = random.randint(1,1000)
out = x * y + 2# witness vector
w = np.array([1, out, x, y])

# check the equality
result = C.dot(w) == np.multiply(A.dot(w),B.dot(w))
assert result.all(), "result contains an inequality"

The size of the matrix depends on w.

However, this is not yet complete, as it lacks security. Please proceed to the next part to learn how to enhance its security.

Ecliptic curve

Why do you need to understand this?

  • zk-SNARKs operate on fields of large numbers within elliptic curves (BN254).

p = 21888242871839275222246405745257275088548364400416034343698204186575808495617

Because for security, any input or witness should not be directly revealed, we utilize BN254, an elliptic curve, to optimize security.

This is the representation of negative one (-1) in Circom.

p = 21888242871839275222246405745257275088548364400416034343698204186575808495617.

# 1 - 2 = -1
(1 - 2) % p

# 21888242871839275222246405745257275088548364400416034343698204186575808495616

Remember that this representation is used for security purposes in Circom.

But why modulo p?

  • To ensure that all values within the circuit remain within a specific range, making it more efficient to reason about and prove their validity in zk-SNARKs.

Okay, no worries if you don't understand yet.

ECDH has multiple ratios (methods to create pairings) - Group Operation - Point Dobublig - Adding Vertical point - Scalar Multiplication πŸ‘ˆ I'll explain this.

Let's say we have...

  • P is a point on curve
  • k is a integer 𝕫
  • Q(P * k time) ----> this is our final destination.

Q = P+P+...+P } k times

Okay, please take a look at this graph.
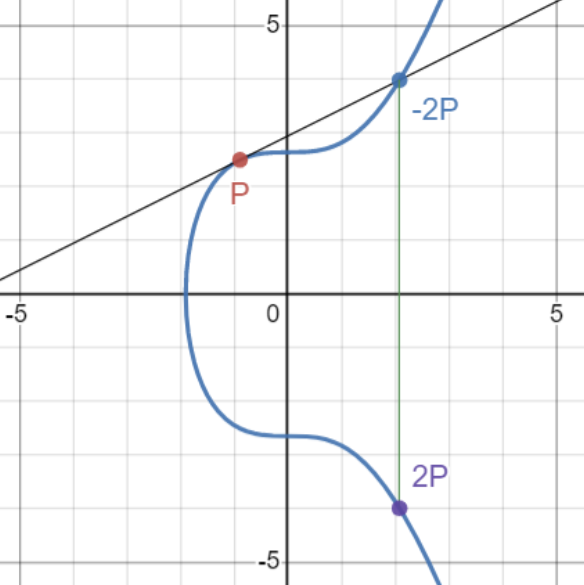
EC Graph

then look into this
EC Point

So, if I ask you what parameter or what is the K value to reach the red point, the answer might be mind-blowing! 🀯

Here is a benchmark of each type of pairing-friendly library. πŸ‘‰ https://hackmd.io/@gnark/eccbench#BN254

Setup Process

Why do we need to set up? - Because we need to ensure that the proof is generated correctly by the prover.

This is type of setup

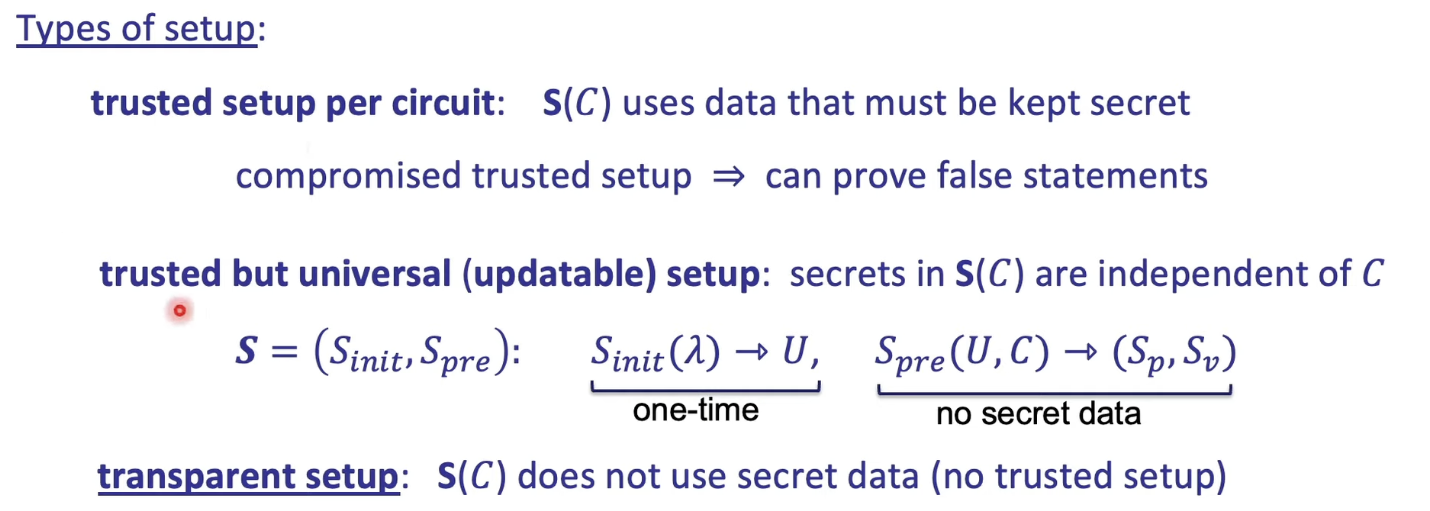
Setup

However, in this section, we will use Groth16 to process the trust setup. It's important to note that this trust setup is specific to each circuit.

You need one setup per circuit.

Here is a code example of the trust setup process.



use ark_bn254::Bn254;
use ark_circom::CircomBuilder;
use ark_circom::CircomConfig;
use ark_groth16::Groth16;
use ark_snark::SNARK;

fn main() {

    let cfg = CircomConfig::<Bn254>::new("main.wasm", "main.r1cs").unwrap();

    let mut builder = CircomBuilder::new(cfg);
    builder.push_input("in", 7);

    // Create an empty instance for setting it up
    let circom = builder.setup();

    // this is random bit that use one time percircuit
    let mut rng = rand::thread_rng(); πŸ‘ˆ
    let params =
        Groth16::<Bn254>::generate_random_parameters_with_reduction(circom, &mut rng).unwrap();


}

Programming concept

HDL it's differ from usually PL.

Programming

Circom

a HDL languages to write circuit

How to Wire Circuits in Circom

  1. Create variables for every intermediate wire.
  2. Write equations to constrain the relationships between the wires.

for example 

pragma circom 2.0.0;

/*This circuit template checks that c is the product of a and b.*/  

template Multiplier2 () {  

   // Declaration of signals.  
   signal input a;  
   signal input b;  
   signal output c;  

   // Constraints.  
   c <== a * b;  
}

Circom