Ecliptic curve
Why do you need to understand this?
- zk-SNARKs operate on fields of large numbers within elliptic curves (BN254).
p = 21888242871839275222246405745257275088548364400416034343698204186575808495617
Because for security, any input or witness should not be directly revealed, we utilize BN254, an elliptic curve, to optimize security.
This is the representation of negative one (-1) in Circom.
p = 21888242871839275222246405745257275088548364400416034343698204186575808495617.
# 1 - 2 = -1
(1 - 2) % p
# 21888242871839275222246405745257275088548364400416034343698204186575808495616
Remember that this representation is used for security purposes in Circom.
But why modulo p?
- To ensure that all values within the circuit remain within a specific range, making it more efficient to reason about and prove their validity in zk-SNARKs.
Okay, no worries if you don't understand yet.
ECDH has multiple ratios (methods to create pairings) - Group Operation - Point Dobublig - Adding Vertical point - Scalar Multiplication 👈 I'll explain this.
Let's say we have...
- P is a point on curve
- k is a integer 𝕫
- Q(P * k time) ----> this is our final destination.
Q = P+P+...+P } k times
Okay, please take a look at this graph.
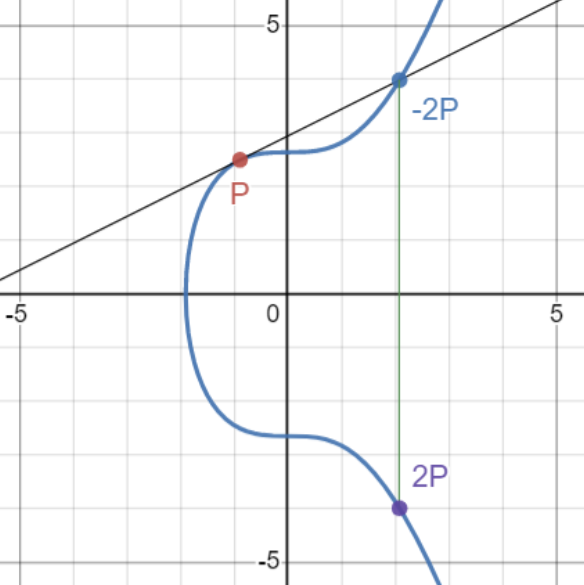
then look into this
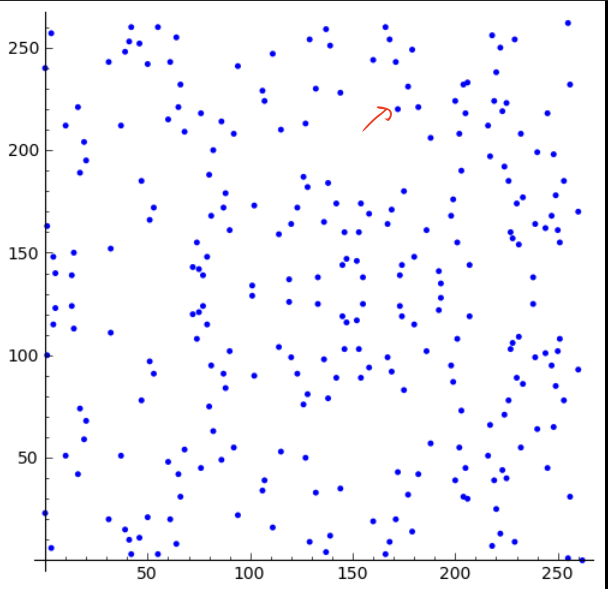
So, if I ask you what parameter or what is the K value to reach the red point, the answer might be mind-blowing! 🤯
Here is a benchmark of each type of pairing-friendly library. 👉 https://hackmd.io/@gnark/eccbench#BN254